CycleGAN for Image-to-Image Translation¶
Today we'll be looking at CycleGANs, a method to train Generative Adversarial Networks to do image-to-image translation.
Examples of Image-to-Image Translation¶
Style Transfer¶
Photo Enhancement¶
Face to Ramen¶

Supervised (Paired) vs. Unsupervised (Unpaired) Training¶
Many image-to-image translation models require training data to come in pairs, the same 'image' in two different styles.
Preparing paired data like this requires a lot of human labor. Often, generating paired datasets for thousands of images is not practical, especially with more complex image translations.
CycleGAN is an architecture to address this problem, and learns to perform image translations without explicit pairs of images. To learn horse to zebra translation, we only require:
- a set $X$ of assorted horse images
- a set $Y$ of assorted zebra images
No one-to-one image pairs are required. CycleGAN will learn to perform style transfer from the two sets despite every image having vastly different compositions.
How CycleGAN Works¶
GAN Recap¶
Recall from our last tutorial that Generative Adversarial Networks learn to generate images using two models:
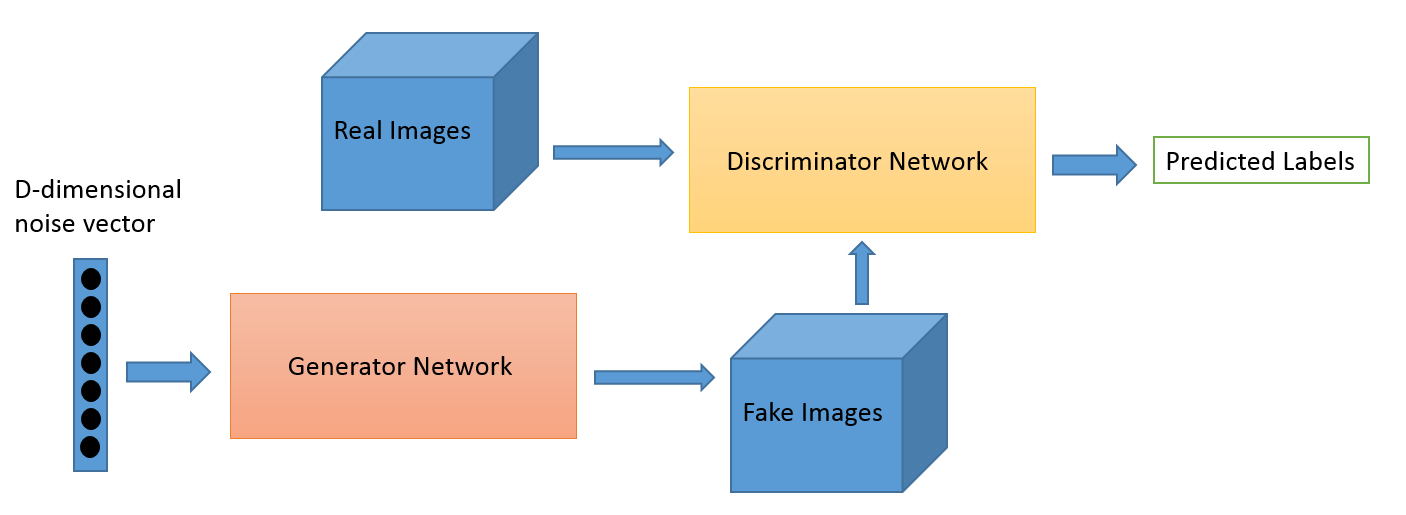
- The Generator model conditions on some inputs and learns to generate an image.
- The Discriminator model scores how 'real' images look, learning to distinguish between generated and real images. This score provides feedback to the generator on how well it is performing, like a teacher grading a student.
- Both models are trained simultaneously, and the feedback loop between the two improves the performance of each other.
- Post-training, the Generator should be able to produce original, realistic looking images.
CycleGAN: Cycle Consistency¶
To learn to translate images of one type to another, CycleGAN uses an intuition called cycle consistency, using two generators and two discriminators. Given image domains X and Y, we have:

- Generator $G: X \rightarrow Y$: translates images from $X$ to $Y$ (e.g. horse to zebra)
- Generator $F: Y \rightarrow X$: translates images from $Y$ to $X$ (e.g. zebra to horse)
- Discriminator $D_X$: scores how real an image of $X$ looks (e.g. does this image look like a horse?)
- Discriminator $D_Y$: scores how real an image of $Y$ looks (e.g. does this image look like a zebra?)
The intuition of cycle consistency is that, if you are able to train these pair of GANs to translate from $X \rightarrow Y \rightarrow X$, i.e. generate images while assuring cycle consistency, that $x \rightarrow G(x) \rightarrow F(G(x)) \approx x$, then you would have learned the image translation task sufficiently well.
Cycle Consistent Loss¶
As you recall, the GAN loss function to assure good quality images is computed with:

CycleGAN introduces a cycle-consistency loss component $L_{cyc}(G, F)$ to assure the property $x \rightarrow G(x) \rightarrow F(G(x)) \approx x$.

The combined loss including GAN and cycle-consistency loss is:

And our objective is to minimize this combined loss for the generator, while maximizing the loss for the discriminator:

CycleGAN Example Results¶
Horse2Zebra, Apple2Orange¶
The model performs very well when it is primarily focused on recoloring images.
Male2Female¶
For gender translation, transfiguration is required rather than simply recoloring. The results aren't perfect, but you can see some reasonable changes being made by the model.

White2Asian¶
Similarly, not perfect with transfiguration here.

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import functools
import torch.nn as nn
def conv_norm_act(in_dim, out_dim, kernel_size, stride, padding=0,
norm=nn.BatchNorm2d, relu=nn.ReLU):
return nn.Sequential(
nn.Conv2d(in_dim, out_dim, kernel_size, stride, padding, bias=False),
norm(out_dim),
relu())
def dconv_norm_act(in_dim, out_dim, kernel_size, stride, padding=0,
output_padding=0, norm=nn.BatchNorm2d, relu=nn.ReLU):
return nn.Sequential(
nn.ConvTranspose2d(in_dim, out_dim, kernel_size, stride,
padding, output_padding, bias=False),
norm(out_dim),
relu())
class Discriminator(nn.Module):
def __init__(self, dim=64):
super(Discriminator, self).__init__()
lrelu = functools.partial(nn.LeakyReLU, negative_slope=0.2)
conv_bn_lrelu = functools.partial(conv_norm_act, relu=lrelu)
self.ls = nn.Sequential(nn.Conv2d(3, dim, 4, 2, 1), nn.LeakyReLU(0.2),
conv_bn_lrelu(dim * 1, dim * 2, 4, 2, 1),
conv_bn_lrelu(dim * 2, dim * 4, 4, 2, 1),
conv_bn_lrelu(dim * 4, dim * 8, 4, 1, (1, 2)),
nn.Conv2d(dim * 8, 1, 4, 1, (2, 1)))
def forward(self, x):
return self.ls(x)
class ResiduleBlock(nn.Module):
def __init__(self, in_dim, out_dim):
super(ResiduleBlock, self).__init__()
conv_bn_relu = conv_norm_act
self.ls = nn.Sequential(nn.ReflectionPad2d(1),
conv_bn_relu(in_dim, out_dim, 3, 1),
nn.ReflectionPad2d(1),
nn.Conv2d(out_dim, out_dim, 3, 1),
nn.BatchNorm2d(out_dim))
def forward(self, x):
return x + self.ls(x)
class Generator(nn.Module):
def __init__(self, dim=64):
super(Generator, self).__init__()
conv_bn_relu = conv_norm_act
dconv_bn_relu = dconv_norm_act
self.ls = nn.Sequential(nn.ReflectionPad2d(3),
conv_bn_relu(3, dim * 1, 7, 1),
conv_bn_relu(dim * 1, dim * 2, 3, 2, 1),
conv_bn_relu(dim * 2, dim * 4, 3, 2, 1),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
ResiduleBlock(dim * 4, dim * 4),
dconv_bn_relu(dim * 4, dim * 2, 3, 2, 1, 1),
dconv_bn_relu(dim * 2, dim * 1, 3, 2, 1, 1),
nn.ReflectionPad2d(3),
nn.Conv2d(dim, 3, 7, 1),
nn.Tanh())
def forward(self, x):
return self.ls(x)
a_real_test = Variable(iter(a_test_loader).next()[0], volatile=True)
b_real_test = Variable(iter(b_test_loader).next()[0], volatile=True)
a_real_test, b_real_test = utils.cuda([a_real_test, b_real_test])
for epoch in range(start_epoch, epochs):
for i, (a_real, b_real) in enumerate(itertools.izip(a_loader, b_loader)):
# step
step = epoch * min(len(a_loader), len(b_loader)) + i + 1
# set train
Ga.train()
Gb.train()
# leaves
a_real = Variable(a_real[0])
b_real = Variable(b_real[0])
a_real, b_real = utils.cuda([a_real, b_real])
# train G
a_fake = Ga(b_real)
b_fake = Gb(a_real)
a_rec = Ga(b_fake)
b_rec = Gb(a_fake)
# gen losses
a_f_dis = Da(a_fake)
b_f_dis = Db(b_fake)
r_label = utils.cuda(Variable(torch.ones(a_f_dis.size())))
a_gen_loss = MSE(a_f_dis, r_label)
b_gen_loss = MSE(b_f_dis, r_label)
# rec losses
a_rec_loss = L1(a_rec, a_real)
b_rec_loss = L1(b_rec, b_real)
# g loss
g_loss = a_gen_loss + b_gen_loss + a_rec_loss * 10.0 + b_rec_loss * 10.0
# backward
Ga.zero_grad()
Gb.zero_grad()
g_loss.backward()
ga_optimizer.step()
gb_optimizer.step()
# leaves
a_fake = Variable(torch.Tensor(a_fake_pool([a_fake.cpu().data.numpy()])[0]))
b_fake = Variable(torch.Tensor(b_fake_pool([b_fake.cpu().data.numpy()])[0]))
a_fake, b_fake = utils.cuda([a_fake, b_fake])
# train D
a_r_dis = Da(a_real)
a_f_dis = Da(a_fake)
b_r_dis = Db(b_real)
b_f_dis = Db(b_fake)
r_label = utils.cuda(Variable(torch.ones(a_f_dis.size())))
f_label = utils.cuda(Variable(torch.zeros(a_f_dis.size())))
# d loss
a_d_r_loss = MSE(a_r_dis, r_label)
a_d_f_loss = MSE(a_f_dis, f_label)
b_d_r_loss = MSE(b_r_dis, r_label)
b_d_f_loss = MSE(b_f_dis, f_label)
a_d_loss = a_d_r_loss + a_d_f_loss
b_d_loss = b_d_r_loss + b_d_f_loss
# backward
Da.zero_grad()
Db.zero_grad()
a_d_loss.backward()
b_d_loss.backward()
da_optimizer.step()
db_optimizer.step()
Our Result: Male2Female¶
Instead of good male-to-female translation, our model learned to apply lipstick to females:


